An Attempt to Value Gold (and A Price Forecast for 2018)
January 30 2018
This week a preliminary attempt to value gold with a different method. I have shown earlier how we can value the stock market: we can compare the replacement value of the underlying company assets with the price we pay for the same assets on the stock market. This ratio is also known as the “equity q ratio,” named after the Tobin q ratio which was first described by Nobel laureate James Tobin (Tobin would take both the equity and debt in his original formulation). This time, I try to do something similar with gold ánd base an initial gold price forecast for this year on our gold q ratio. But there remains plenty of work to do. If you feel prompted to contribute and collect data and assist me, please do not hesitate to let me know.
The Replacement Value of Gold
We want a troy ounce gold bar. How can we get one? We can either by the bar on the market (against current market prices) or we can mine and melt the gold ourselves. Now, the latter might sound rather sensational or a little bit too optimistic, but there is a grain of truth in it.
Mining and melting “our own bar of gold” is in fact the replacement value of gold. And despite we might not be able to actually mine the gold ourselves, other third (professional) parties can do it if the price differential to the market price is sufficiently large enough. And vice versa. If the replacement value of gold exceeds the market price, then why not simply buy bullion on the market? Thus, there exists a regression to the mean: the replacement value of gold can never exceed by much the market price of gold.
This is, of course, nothing new. It is the same principle as we have applied earlier to the stock market and which led James Tobin a Nobel prize in economics. Let us explain step by step our gold q ratio.
The replacement value of gold can roughly be determined by assessing, first, the cost of buying a mine and, second, mine the gold. Now, there exist many different ways to measure the cost of mining gold. Better said, something called “cash cost” is already often reported by gold miners (which equals the necessary cash outlays to get an ounce of gold out of the ground). But this “cash cost” does not include (a) depreciation of fixed assets (machines, et cetera), (b) general and administrative expenses of the mining company, and (c) other overhead costs which are as good as inevitable in operating the gold mine. This “cash cost” is therefore not a correct reflection of our gold replacement value.
“All-in sustaining cost” is an alternative that was presented by the World Gold Council and other gold companies. With this alternative they attempted to create a standardized measure, which allows for direct comparisons between gold miners. This alternative does include capital expenditures (or CapEx, at least if it is directly related to the extraction of the gold) and general and administrative expenses as well. But gold miners are surprisingly creative in moving expenditures around from, let´s say, “relevant” to “not relevant” CapEx. A computer more or less would not make a lot of difference, but marking a Caterpillar truck to move the gold mined as “not directly related to the mining of the gold” seems to be a stretch. In this case, “all-in sustaining cost” would be somewhat lower. Last but not least, it is possible to take the cost of sales of gold and to divide gold sales by this cost of sales measure (cost of goods sold) to get an indication of cost per troy ounce.
The problem with all these measures is the fact that it does not take into account the cost to actually buy a share in the mining company (which is quite an omission if we want to compare the current gold price against its true replacement value). Let us see how this would work if we take one of the world´s largest gold mining companies, Barrick Gold Corp.
For the full year 2016, Barrick Gold Corp reports that its “all-in sustaining mining cost” equals $730 per troy ounce. At that all-in sustaining cost, they reached a total annual production of 5.517 million ounces in 2016 and, in addition, they report to have 85.9 million ounces in proven gold reserves (in the ground, though). That means that at a rate of about 6.5% Barrick is taking its proven reserves out of the ground, which without new exploration and new mining projects would give us a lifespan of about 15 years.
Against the current $730 (we assume that this number does not change) to mine a troy ounce of gold, it will cost a total of approximately $62.7 billion to mine the entire 85.9 million ounces in proven reserves. Moreover, Barrick has 1,116 million (almost 1.2 billion) shares outstanding against a market price of $14.50 per share at the end of 2016. This means that we pay $14.50 for roughly 0.074 ounces in proven gold reserves or 13.57 shares (multiplied by the same $14.50 per share would give us $196.77) for every ounce of gold in the ground.
But those $196.77 would imply that we have the cost already in our hands as of today, while in fact the gold will be mined bit by bit every year over a period of, roughly, 15 years (after all, we are talking about reserves in the ground). Therefore we will have to calculate the future value of $196.77 as to take into account the time value of money, and we do so with the current rate of extraction (6.5% per year) and a lifespan of 15 years. Hence:
(1) 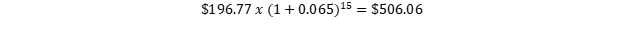
To this amount, we add the all-in sustaining cost of Barrick ($730) to arrive at:
(2) 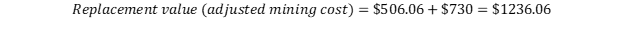
As alternative, we can also take the cost of sales (of gold) of $790 per troy ounce instead of the all-in sustaining cost, which would give us:
(3) 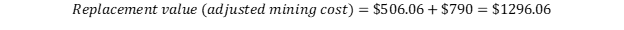
This leads us to our gold q ratio (inspired by Tobin’s q):
(4) 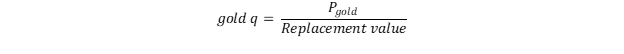
Where:
Pgold = the market price of gold
Replacement value = our estimated replacement value of gold
In our example, with all inputs of Barrick for the full year 2016 and with the gold price at the end of 2016, we get the following:
(5) 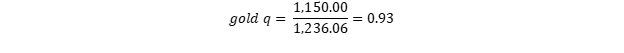
This would mean a relative undervaluation (1 < q). And indeed: it turns out that the gold price rose from $1,150/oz to over $1,300/oz since 2016, which is, as you might recall, the period in which we collected our data inputs. Ever since that data, the average annual return (which includes both 2016 and 2017) equaled a surprisingly high 11.35%, higher than the average annual return since 1970 (7.9%) and many times higher than the average annual return on gold since 1980 (1.9%).
For 2018, we could take Barrick Gold Corp´s most recent share price ($14.80) and the current gold price. This would give us the following:
(6) 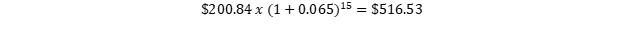
With Barrick’s most recent guidance on its all-in sustaining cost per troy ounce ($720 per troy ounce) we would get:
(7) 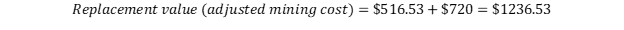
We arrive again at our gold q and use the most recent gold price (January 25, 2018). This leads us to:
(8) 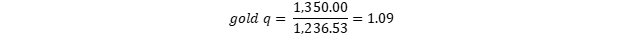
What indicates relative overvaluation (q > 1). In this case, the expected future return on gold would either be low or negative (or, that is of course a possibility, positive but even more positive for gold mining shares).
We could also take the interest rate and/or gold basis (the spread between the spot gold price and the future gold price) as the discount rate to not only weigh in the rate of extraction (the earlier mentioned 6.5%) but also the time value of money. This would give us a, at any rate, higher replacement value of gold and thus a lower gold q ratio.
Now, our model has a few shortcomings. I have only used one single gold mining company (Barrick Gold Corp), only one data point (end of 2016), and many other implicit choices which eventually affect our q measure. We could, for instance, take the average share price of Barrick over 2016 instead of share price at year-end. We could take the cost of sales instead of the all-in sustaining cost. We could include all major mining companies instead of just one. We could account for exploration by estimating an average growth in proven reserves (for the whole gold mining industry) and including this growth in our replacement value estimate. All these factors, however, become trivial when we would use a longer time series with a weighted average instead of our assumption that replacement value equals the gold market price one on one. Historically, average gold q could be around 0.9 for instance, instead of 1, with as a result that the role of factors as the ones we mentioned earlier would more or less vanish (if we assume that these factors, over time, remain equal or stable).
The problem with gold is, however, (and the same applies to other monetary assets with relatively stable supply curves, such as Bitcoin) that corrections in q (the “regression to mean q”) can come from two sides. Share prices of mining companies could rise and increase our estimated gold replacement value (to reflect the new, higher market prices of gold). This is something that we should actually expect to occur as long as stock market investors view the rally in gold prices as something sustainable instead as something temporarily.
On the other side, gold prices could fall to replacement value. Or, in a more extreme case, mining companies might decide to close marginal gold mines, which would lead to a reduction in the all-in sustaining cost per troy ounce. This is, at any rate, no reason for concern: it is rather silly to close gold mines when the gold price per troy ounce exceeds the replacement value of gold per troy ounce.
For the future, we will need a time series with a larger number of publicly listed mining companies, an average q, and the 3-year and 5-year expected returns on gold for q in different quartiles. Moreover, the data should reveal whether regressions to the mean (corrections toward q) have historically occurred on the “gold price side” or on the “replacement value side”, besides figuring out what the drivers were of such corrections or regressions to the mean.
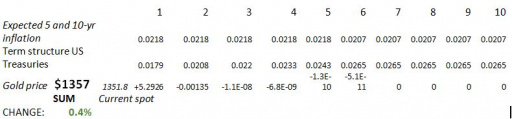
I also tried another model. As I have showed earlier in response to an article published by Lawrence Summers (1988), we could also view the gold price as the inverse of the interest rate. Summers showed that when returns on capital markets are low, returns on gold tend to be high. This relationship is quite stable. Any increase in gold prices would simply be the inverse of the negative real returns on capital markets. When real returns are positive, gold prices would fall. This approach, however, appears to be doomed to fail and seems to yield no sensible valuation. A model I developed deduced from Summers´ 1988-paper, leads to very slight changes and forecasts that (in this case, a price increase of 0.4%) do no justice to the real observed price volatility of gold.
Conclusion
This is a call to think along. Suggestions and input are very much welcome. If someone is willing to do the hard work (or happens to possess the right data) to gather a solid dataset for estimating the replacement value of gold, then I would be happy to hear from you.
In case you are only interested in my (preliminary) conclusions, then that is of course also possible. It appears, on the basis of our present analysis, that the gold price has some downside, something I repeated on earlier occasions. But q might also mislead us, if gold mining shares or production costs rise rapidly. In that case the gold price will not fall. At any rate, the overvaluation – if it exists – is many times smaller than the overvaluation on the US stock market. I would therefore bet my money on gold for the coming years, regardless of (some) possible downside in the short run.Attachments:
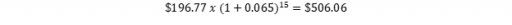
1

2

3

4
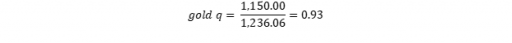
5
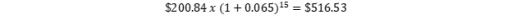
6

7
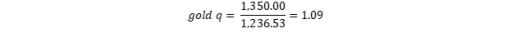
8